Cette semaine, je me suis intéressé aux données spatio-temporelles. Plusieurs raisons justifient le fait que je me sois penché le sujet. D’abord, la Ville de Montréal rend disponible des données ouvertes en lien avec différentes sphères d’activité : économie et entreprises, éducation, santé, société et culture. Le secteur qui m’intéresse en particulier pour Montréal est celui des transports.

Le CRIM a déjà eu à travailler avec des données spatio-temporelles pour prédire le temps de réponse des pompiers du Service de sécurité incendie de Montréal. L’article traitant du sujet se retrouve d’ailleurs sur Medium. Compte tenu de l’expérience acquise lors de ce projet, il semblait logique de poursuivre l’étude du sujet. Ces nouvelles connaissances pourraient éventuellement être appliquées à la résolution d’autres problèmes liés à la mobilité, par exemple les déplacements à Montréal,
grâce aux données récoltées par l’application MTL Trajet ou les caméras et détecteurs dispersés sur l’île de Montréal.

Les données spatio-temporelles offrent aussi un potentiel intéressant d’un point de vue local pour la prévention des inondations au Québec. Le Ministère de la Sécurité publique a dévoilé en 2018 un Plan d’action en matière de sécurité civile relatif aux inondations pour faire suite aux importantes crues printanières de l’année précédente. Une enveloppe de plus de 30 M$ sur 5 ans a été prévue afin de mettre à jour la cartographie des zones inondables sur le territoire québécois. En climatologie, les données spatio-temporelles sont devenues un outil si important que de nombreux projets en science des données se développent pour les organiser, les analyser et les interpréter.

Les données spatio-temporelles

Les données spatio-temporelles sont collectées dans plusieurs domaines : en science du climat, pour prédire la naissance d’événements météorologiques extrêmes, en science de la Terre, pour détecter des zones d’anomalies au sein d’environnements marins, ou en épidémiologie, pour étudier la propagation de maladies. D’autres domaines comme la neuroscience, la science de l’environnement, les médias sociaux et la dynamique des trafics utilisent aussi ce type d’information à toutes les sauces.

Mais quelle est la particularité des données spatio-temporelles? Elles sont caractérisées par des attributs spatiaux (distance, direction, position) et temporels (nombre d’occurrences, changements dans le temps, durée). En d’autres termes, il s’agit de données, ou de mesures, qui subissent un changement dans le temps et dans un l’espace.

Par exemple, pour la prédiction d’événements météorologiques, la représentation spatiale est définie par un quadrillage de la région terrestre étudiée, et caractérisée par divers paramètres et mesures atmosphériques. La représentation temporelle est ensuite définie par l’évolution de ces paramètres dans le temps, ce qui pourrait permettre, par exemple, de concevoir un modèle de prédiction de l’évolution d’ouragans.

La littérature sur le sujet est abondante : la diversité de modèles, d’approches et d’applications est innombrable. Pour commencer, je me suis donc limité à quatre articles semblant intéressants pour me donner une idée de la manière de gérer et d’utiliser les données spatio-temporelles.

Le premier article présente une approche utilisant un réseau de neurones convolutifs 3D pour apprendre des caractéristiques (features) spatio-temporelles. Le deuxième présente des applications d’exploration de données (data mining) par règles d’association dans un contexte d’analyse d’ouragans. Le troisième traite d’un modèle d’apprentissage de structures hiérarchiques pour prévoir le déclenchement d’événements météorologiques extrêmes. Le quatrième définit un modèle de data mining spatio-temporel pour l’analyse de structures d’association anormales dans un environnement marin. Les sections suivantes présenteront une courte synthèse des idées et concepts essentiels et pertinents provenant de chaque article.

Learning Spatiotemporal Features with 3D Convolutional Networks

Tran, D., Bourdev, L., Fergus, R., Torresani, L., & Paluri, M. (2015, December). Learning spatiotemporal features with 3d convolutional networks. In Computer Vision (ICCV), 2015 IEEE International Conference on (pp. 4489–4497). IEEE.

Objectif

Conception d’une approche pour l’apprentissage de features spatio-temporels utilisant un réseau de neurones convolutifs profond en trois dimensions (3D ConvNets) entraîné sur un jeu de données à grande échelle de vidéos supervisés. Le but étant de parvenir à reconnaître différents types d’action (101 actions) et objets (42 types), et de classifier des paires d’actions similaires (432 actions) ou des scènes individuelles (14 scènes).

Sommaire

L’idée derrière les opérations de convolution 3D est de préserver l’information temporelle d’un signal d’entrée. En effet, les convolutions 2D appliquées sur une ou de multiples images génèrent une image également, donc une sortie en deux dimensions. Seules les convolutions 3D préservent l’information temporelle et génèrent une sortie volumique. Le même phénomène est observé pour les étapes de pooling, en 2D et 3D respectivement. Ainsi, l’idée derrière l’utilisation des convolutions 3D est d’encapsuler l’information en lien avec les objets, les scènes et les actions.

Méthode

Architecture

L’architecture de base du kernel de convolution est un champ réceptif fixe de dimension {d x 3 x 3} où seule la dimension temporelle est modifiée pour fin d’expérimentation. La raison pour cette limitation est le temps d’entrainement très important qui découlerait de nombreuses expériences. La notation pour les dimensions des clips vidéos et des kernels est la suivante :

Clip vidéo (c x l x h x w)

c est le nombre de canaux (différentes perspectives d’une image, nombre de matrices la définissant), l est le nombre d’images, h est la hauteur, w est la largeur

Kernel (d x k x k)

d est la dimension temporelle, k est la dimension spatiale (hauteur et largeur identique)

Paramètres de base

Des vidéo-clips sont pris en entrée pour ensuite réaliser une reconnaissance ou une classification de ceux-ci. Les vidéos ont une dimension de 128 x 171 et sont séparés en clips de 16 images. Chaque image est divisée en 3 canaux (RGB). Plusieurs paramètres sont modifiables de manière à obtenir les meilleurs résultats possibles : nombre de couches de convolution, couches de pooling, couches entièrement connectées, couches de perte, filtres par couche, et le remplissage, la foulée (stride), la dimension du pooling, la taille du lot (batch size), le taux d’apprentissage (learning rate) et le nombre d’itérations.

Variation des paramètres

Plusieurs configurations de paramètres sont testées pour optimiser l’encapsulation de l’information temporelle. Par souci d’économie de temps, seulement la profondeur temporelle d du kernel est modifiée. Deux approches sont empruntées :

Profondeur temporelle homogène

Toutes les couches de convolutions utilisent des kernels de dimensions temporelles identiques. Quatre configurations sont testées, avec des profondeurs respectives de {1, 3, 5, 7}. Par exemple, 1–1–1–1–1 pour une architecture à cinq couches convolutives, où chaque kernel à chaque couche possède une profondeur de 1.

Profondeur temporelle variable

La profondeur temporelle du kernel varie selon la couche de convolution. Deux configurations sont testées, croissante et décroissante, respectivement de la forme suivante : 3–3–5–5–7 et 7–5–5–3–3, pour des architectures à cinq couches convolutives.

Pour les architectures homogènes, celle avec une profondeur de trois (3–3–3–3–3) fournit les meilleurs résultats. Comparée aux deux architectures hétérogènes, elle est plus performante. Il est aussi démontré qu’une augmentation du champ spatial n’améliore pas les résultats. L’architecture 3 x 3 x 3 est donc retenue pour le dimensionnement des kernels.

Architecture finale

En réponse aux expériences précédentes et en considérant les limites de calcul et de mémoire du matériel disponible, le réseau de neurones convolutifs 3D se présente sous la forme suivante.

Le 3D ConvNets contient 8 couches de convolution, possédant respectivement {64, 128, 256, 256, 512, 512, 512, 512} filtres. Ces couches de convolution permettent de transformer les images et apprendre différents features. Chaque kernel est de dimension {3 x 3 x 3} et possède une foulée de {1 x 1 x 1}.

Le réseau contient 5 couches de max-pooling, opération où seule la valeur maximale d’une région délimitée par un kernel est retenue pour réduire la dimensionnalité de la matrice d’entrée. Les kernels pour les couches {pool2, pool3, pool4, pool5} sont de dimension {2 x 2 x 2} et {1 x 2 x 2} pour la couche pool1. Ils possèdent tous une foulée de {1 x 2 x 2}.

Deux couches entièrement connectées possédant 4096 unités de sortie succèdent aux opérations de convolutions et pooling. Elles sont nécessaires pour classifier les images à partir des features haut-niveau fournis par les étapes de convolution.

Résultats

Le 3D ConvNets est testé sur la classification d’actions humaines, la similarité de paires d’actions, et la reconnaissance de scènes et objets.

Le 3D ConvNets est mieux adapté aux données spatio-temporelles qu’un 2D ConvNet. Il détecte mieux l’information en lien avec l’apparence et le mouvement.
Une architecture homogène {3 x 3 x 3} des kernels de convolution, pour chaque couche, donne les meilleures performances.
Les features appris par le réseau, avec un simple classificateur linéaire, surpassent ou sont comparables à ceux appris par les méthodes courantes lorsque le réseau est testé sur 4 cas d’application différents.
Le réseau est très simple à utiliser.
Le 3D ConvNet se concentre d’abord sur l’apparence dans les premières images, puis traque les mouvements dans les autres.

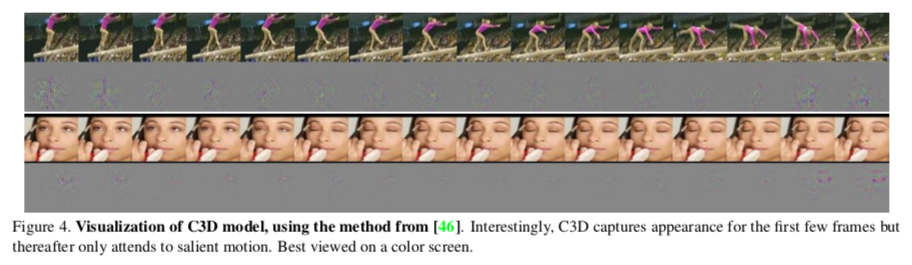
Les features appris par le 3D ConvNets sont compacts et descriptifs, comme les résultats le démontrent suite à une diminution de la dimensionnalité grâce à une Principal Component Analysis (PCA).
Les features montrent une bonne capacité de généralisation.

Association Rule Data Mining Applications for Atlantic Tropical Cyclone Intensity Changes

Yang, R., Tang, J., & Sun, D. (2011). Association rule data mining applications for Atlantic tropical cyclone intensity changes. Weather and Forecasting, 26(3), 337–353.

Objectif

Application d’une technique de data mining, l’exploration de règles d’association (Association Rule Data Mining), pour l’analyse de changements d’intensité de cyclones tropicaux (TC). L’article fournit un guide d’utilisation pour cette technique d’exploration et une méthode pour surmonter le faible nombre d’occurrences de certaines conditions météorologiques extraites pour améliorer la capacité de prédiction de l’intensité des tempêtes tropicales.

Aperçu

La technique d’association rule mining fournit une image détaillée du jeu de données et permet la détection de relations parmi de multiples conditions pouvant être omises par une approche d’analyse théorique. Le but de l’étude est d’appliquer cette technique de data mining de manière non supervisée et automatique. Cette exploration fournit des associations “multiple to one” à partir d’une grande diversité de caractéristiques géophysiques décrivant des cyclones s’intensifiant, s’affaiblissant ou stables. Les résultats de l’exploration de données peuvent permettre de mettre en lumière les mécanismes physiques sous-jacents qui influencent les changements d’intensité des tempêtes tropicales.

Données et méthodologie

Jeux de données

Le jeu de données HURDAT (NHC’s North Atlantic Hurricane Database) a été utilisé pour classifier l’intensité des cyclones et leur position. Le jeu de données SHIPS 2003 a été utilisé pour obtenir divers paramètres concernant les tempêtes tropicales (21 features). La technique d’association rule implémentée par Borgelt a été appliquée sur le jeu de données par la suite.

Définitions

Une règle d’association se présente sous la forme suivante : Z ← X, Y. Dans un contexte commercial, un exemple de règle serait de dire qu’un client achetant l’item X et Y est aussi propice à acheter l’item Z. Les items X et Y sont appelés des antécédents et Z est appelé le conséquent.

Dans le contexte de l’article, les antécédents sont les conditions géophysiques des TC représentées par un intervalle de valeurs et le conséquent est une catégorie de changement d’intensité (intensifiant, affaiblissant, etc.).

Trois paramètres sont typiquement utilisés pour l’exploration des règles d’association. Le support estime la probabilité P( { X, Y, Z } ), soit, par exemple, la fréquence à laquelle les conditions particulières pour des tempêtes tropicales (vitesse du vent élevée/basse, pression élevée/basse, etc.) apparaissent dans le jeu de données. La confiance estime la probabilité P( Z | { X, Y } ), soit la fréquence à laquelle les conditions particulières de tempêtes tropicales ont bel et bien occasionné un changement d’intensité Z. Une règle d’association est forte si elle possède un support et une confiance élevés.

Le lift estime la probabilité P( { X, Y, Z } ) / [ P( { X, Y } ) x P( Z ) ], soit le ratio du support calculé précédemment sur celui qui serait attendu si les conditions X et Y étaient indépendantes. En d’autres termes, le lift donne le ratio entre la probabilité réelle qu’un ensemble d’items contienne l’antécédent et le conséquent, divisé par le produit des probabilités individuelles de l’antécédent et du conséquent. C’est le ratio de la confiance sur la confiance attendue.

Un lift de 1 impliquerait que la probabilité d’occurrence des antécédents et du conséquent est indépendante. Un lift plus grand que 1 impliquerait que la probabilité d’occurrence des antécédents et de leur conséquent est dépendante.

Un exemple de règle d’association sera expliqué plus bas pour faciliter la compréhension du concept.

Stratification des cyclones et pré-traitement des données

Stratification

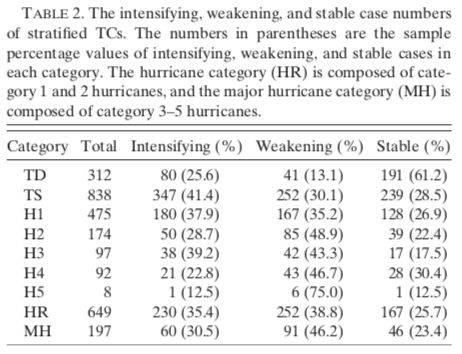
Puisque les changements d’intensité des cyclones tropicaux dépendent de l’intensité initiale de ces cyclones, l’ensemble de données est divisé en différents groupes. Mais avant de stratifier le jeu de données, il est nécessaire de retirer les cyclones ne possédant pas un ensemble de paramètres complet. Ensuite, les cyclones peuvent être groupés selon leur intensité initiale. Ces groupes incluent :

Dépressions Tropicales (TD)
Tempêtes Tropicales (TS)
Ouragans (H1, H2, H3, H4, H5)

Deux autres catégories sont ajoutées, car les ouragans de classe 5 sont peu nombreux. Il est difficile de définir des règles avec un échantillon aussi petit, c’est pourquoi un groupe contenant les ouragans de classe 1–2 et un autre contenant les classes 3–5 sont créés.

Groupe d’ouragans mineurs (HR)
Groupe d’ouragans majeurs (MH)

Pour explorer les combinaisons de facteurs influençant les changements d’intensité, les cyclones sont séparés selon qu’ils s’intensifient, s’affaiblissent ou demeurent stables (voir Table 2).

Pré-traitement

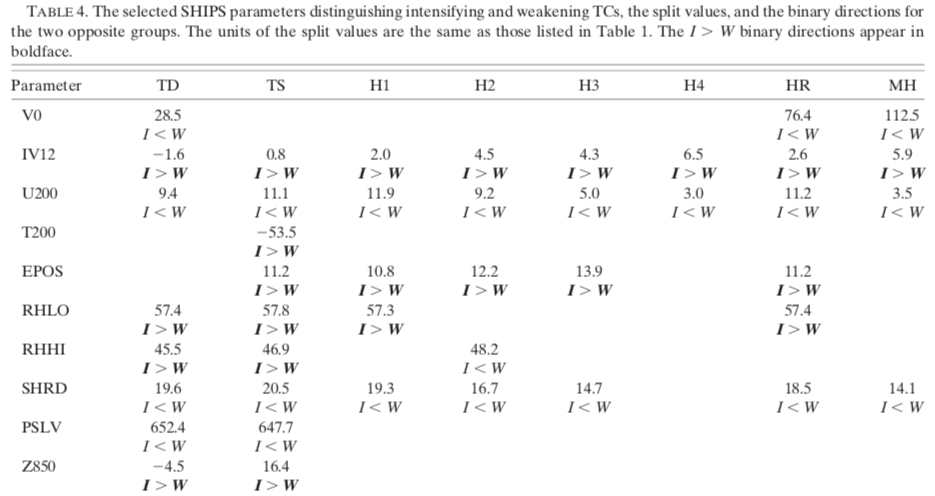
À l’origine, l’algorithme d’association rule mining est conçu pour traiter des jeux de données contenant des attributs de type booléen. Dans le cas présent, les attributs des cyclones sont numériques et continus. Par conséquent, il est essentiel de les transformer en conditions binaires. Le spectre de valeurs est donc divisé en deux groupes : faibles valeurs et hautes valeurs, selon un seuil prédéfini.

Le seuil pour chaque paramètre est estimé en prenant la moyenne de la moyenne respective des cyclones s’intensifiant et s’affaiblissant, et ce, pour chaque catégorie de cyclones. La relation I > W (en gras) indique que la moyenne des cas s’intensifiant est considérablement plus grande que celle des cas s’affaiblissant, et vice versa. Cette expression permet déjà d’avoir un aperçu du rôle de chaque paramètre dans l’intensification ou l’affaiblissement des cyclones.

Association Rules

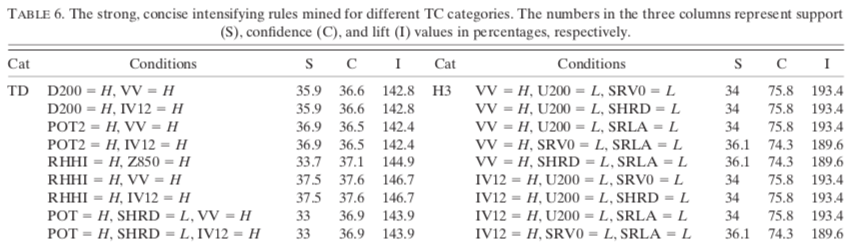
L’algorithme d’association rule mining implémenté par Borgelt a été appliqué avec les paramètres binaires transformés comme antécédents pour tenter de trouver des combinaisons liées aux cyclones s’intensifiant, s’affaiblissant et stables. Les abréviations H et L sont utilisées pour représenter les valeurs de paramètres élevées et basses. Par exemple, U200 = L pour le cas TS signifie que le vent zonal de 200-hPa est moindre ou égale à 11,1 kt.

À priori, les paramètres de contrôle de la force des règles sont fixés à 33 % pour le support et la confiance, et 100 % pour le lift. Voici comment interpréter une règle d’association.

Une règle a typiquement la forme suivante :

INTENS ← U200 = L, SHRD = L, SRLA = L (38,7, 75,4, 138,9)

Cela signifie que, lorsque les trois conditions (U200 = L, SHRD = L, SRLA = L) sont satisfaites, une tempête va s’intensifier avec un support de 38,7 %, une confiance de 57,4 % et un lift de 138,6 %.

En d’autres termes, pour les cyclones dans la catégorie Tempêtes Tropicales (TS), 38,7 % des cas satisfont les conditions (U200 = L, SHRD = L, SRLA = L). Parmi ces cyclones, 57,4 % se sont intensifiés par rapport à l’échantillon moyen de 41,4 % s’intensifiant. Le lift représente le ratio de la confiance sur la confiance de l’échantillon moyen s’intensifiant (57,4/41,4 = 138,6 %).

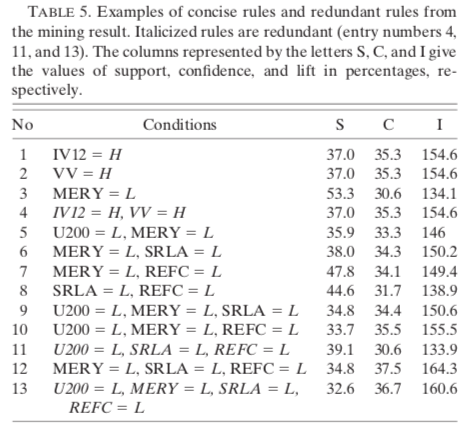
Cependant, il est nécessaire de retirer les règles redondantes suite à l’application de l’algorithme pour seulement considérer les règles concises. Une règle est concise si elle ne peut être dérivée par un sous-ensemble d’antécédents provenant d’une autre règle possédant une confiance plus élevée. En d’autres termes, une règle concise contient le plus petit nombre d’antécédents. Toute règle contenant les mêmes antécédents et des antécédents supplémentaires, mais n’obtenant pas une confiance supérieure à celle d’une règle concise est une règle redondante.

Par exemple, la règle 4 (voir Table 5) est redondante, car elle possède la même confiance que la règle 1 et 2. La règle 11 est redondante, car elle contient une combinaison de conditions apparaissant dans la règle 8 et possède une confiance plus faible que celle-ci.

Intramural Binding

Certains paramètres couvrent le même processus physique: par exemple, IV12 et VV quantifient le changement d’intensité passé d’un cyclone. D’autres sont tous associés au cisaillement vertical : U200, SHRD, SRV0 et SRLA. Lorsque les valeurs d’un paramètre peuvent être utilisées pour prédire les valeurs d’un autre, on dit qu’ils sont intramurally bounded.

Pour révéler ces liaisons, les association hyper-edges ont été générés grâce au même algorithme d’association rule mining. Les résultats ont bel et bien démontré une liaison parfaite entre IV12 et VV pour toutes les catégories sauf le groupe MH, et une forte liaison entre U200, SHRD, SRV0 et SRLA. Voici donc une autre contribution intéressante provenant de cette technique de data mining.

Résultats

Cette étude a démontré que l’association rule mining peut être utilisé dans le domaine de la géoscience avec succès.

Facilité d’interprétation des résultats.
Des combinaisons de paramètres ont pu être révélées, permettant de regrouper des conditions favorisant l’intensification ou l’affaiblissement des cyclones.
Un mouvement de cyclone plus rapide vers le nord favorise l’intensification des tempêtes tropicales, mais pas celle des ouragans.
Les tempêtes tropicales s’intensifiant sont plus fortement associées à une haute convergence dans l’atmosphère supérieure (200-hPa relative eddy momentum flux convergence) que celles s’affaiblissant, alors que les ouragans s’intensifiant sont plus fortement associés à des valeurs de convergence inférieures.
Les combinaisons de conditions identifiées fournissent de plus hautes probabilités de voir une intensification/affaiblissement que celles basées sur une seule condition (typique des études statistiques traditionnelles).
Cette étude va permettre une amélioration de la prévision de l’intensité des cyclones (TC).

A Hierarchical Pattern Learning Framework for Forecasting Extreme Weather Events

Wang, D., & Ding, W. (2015, November). A hierarchical pattern learning framework for forecasting extreme weather events. In Data Mining (ICDM), 2015 IEEE International Conference on (pp. 1021–1026). IEEE.

Objectif

Conception d’un modèle pour découvrir des structures (pattern) au sein d’un système spatio-temporel dans le but de prévoir des événements météorologiques extrêmes. Les structures sont découvertes de manière hiérarchique, c’est-à-dire qu’à chaque niveau d’apprentissage, de nouvelles caractéristiques contextuelles sont apprises et utilisées par le niveau suivant. Plusieurs difficultés doivent être surpassées pour traiter un tel système :

La taille massive de l’espace de caractéristiques (feature space).
La présence de structures complexes au sein du système spatio-temporel.
Les requis sévères au niveau de l’interprétabilité du modèle : nous voulons comprendre, pas seulement prédire.

Sommaire

Résumer l’évolution temporelle des variables individuelles. À chaque position, les changements temporels d’un paramètre sont généralisés en une caractéristique unique.
Résumer les relations spatiales pour assembler les caractéristiques singulières en regroupements.
Résumer les relations intervariables pour prévoir les événements extrêmes.

Définitions

Caractéristique et ensemble de caractéristiques

Une caractéristique (feature) se présente sous la forme d’un tuple {L, T, V}. V est une variable du domaine. L indique la position (x, y). T indique le temps de l’échantillonnage.

Un ensemble de caractéristiques (feature set) est une variable échantillonnée sur un intervalle de temps. Une variable échantillonnée d’un temps T1 à T4 sera considérée comme un feature set de la forme {V1, V2, V3, V4}.

Structure et structure basée sur la position

Une structure (pattern) X est un ensemble de paires feature-value correspondant à un ensemble de caractéristiques. C’est une règle construite à partir de valeurs de feature possibles pour un certain ensemble. Par exemple, X = {< V1, 1 >, < V2, 0 to 4 >, < V3, 1 or 2 >, < V1, 3 >}.

Une structure basée sur la position (location-based pattern) se présente sous la forme d’un tuple {X, L}. X représente un pattern et L contient l’information spatiale de la structure.

Support et ratio de croissance

Un pattern X est supporté par une instance I provenant d’un ensemble de données D si les valeurs des features de l’instance I sont conformes à la règle spécifiée par le pattern X. Le support d’un pattern X est le nombre d’instances I provenant d’un ensemble de données D qui le supporte, divisé par le nombre total d’instances I dans D. En d’autres termes, le support est une indication de la fréquence à laquelle un pattern X apparaît dans un ensemble de données D.

Si l’on divise D en deux partitions {Dp, Dn}, le ratio de croissance d’un pattern X est le ratio du support de X dans la partition Dp par rapport au ratio du support de X dans la partition Dn.

Caractéristique d’une structure

La caractéristique d’une structure (feature of pattern) X est une variable binaire indiquant si le pattern est présent ou non dans une instance I.

Méthode

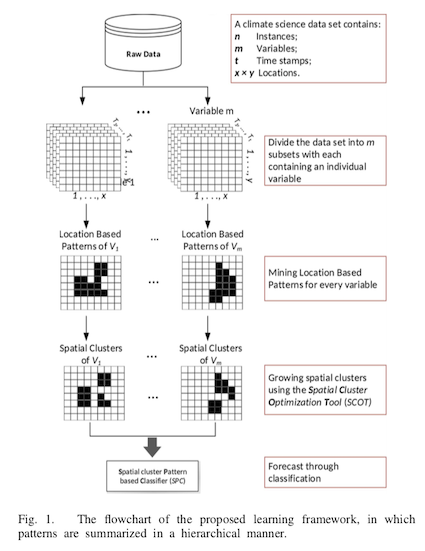
Apprendre les structures basées sur la position

Le premier algorithme basé sur du pattern-mining par contraste sert à apprendre les location-based patterns. Pour commencer, l’ensemble de données est partitionné en m sous-ensembles, chacun contenant une variable, puis les structures basées sur la position sont apprises (ligne 3). Les patterns sets sont générés séparément pour chaque sous-ensemble et pour chaque position au sein de ceux-ci (ligne 4–8). À chacune de ces positions, les ensembles de structures appris sont généralisés en une structure singulière représentative, qui est ensuite transformée (ligne 9). Par exemple, pour une position (x, y), l’ensemble de patterns {p1, p2, …} d’une variable V représente l’ensemble de changements temporels révélateurs qui sont survenus plus fréquemment que les autres dans une partition de l’ensemble de données.

Former les regroupements spatiaux

Pour ce deuxième algorithme, les régularités spatiales du système sont généralisées en agrandissant les location-based patterns appris précédemment en regroupements (clusters) spatiaux. Chaque variable est traitée séparément (ligne 2–3). Pour une variable V1, un feature F est récupéré dans son ensemble de structures basées sur la position (ligne 5) et un ensemble N contenant tous les voisins spatiaux de F est créé (ligne 6). Pour tous les features f dans N, deux conditions sont testées en liant avec le support et le ratio de croissance de la structure jointe f ∩ F (ligne 9). Si les conditions sont satisfaites, les structures f et F sont combinés en un nouveau feature et l’ensemble de voisins est mis à jour en ajoutant les voisins de f dans N (ligne 10–11).

Prévoir par une classification

Le dernier algorithme examine les interactions entre les différentes variables en développant un Spatial cluster Pattern-based Classifier (SPC), un algorithme d’apprentissage basé sur les instances. Une instance est classifiée en analysant ses structures au sein des regroupements spatiaux (ligne 3–4) et en calculant le ratio de croissance des structures (ligne 5–9). S’il est plus élevé que le seuil prédéfini, l’instance est classée positivement.

Résultats

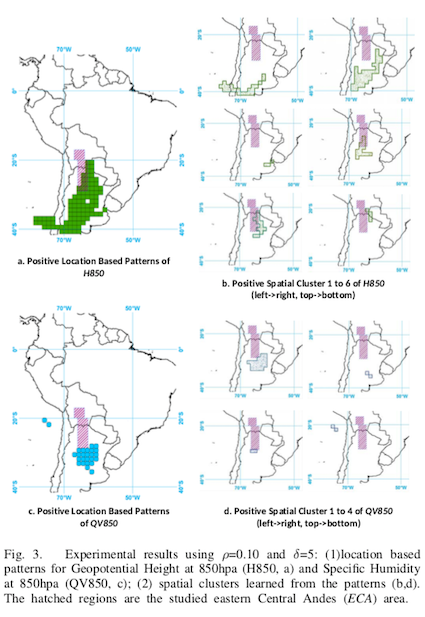
Les patterns appris grâce à l’approche de cet article vont de pair avec les connaissances provenant d’études dans le même domaine.
L’augmentation des seuils de support et ratio de croissance a augmenté la valeur F1.
Prévoir en utilisant des caractéristiques de regroupements spatiaux (SCF) a donné de meilleurs résultats qu’en utilisant simplement des caractéristiques de structures basées sur la position (LPF).
Les SCF réduisent le risque de surapprentissage (overfitting) et fournissent un meilleur ratio de croissance, au profit du support.

A spatiotemporal mining framework for abnormal association patterns in marine environments with a time series of remote sensing images

Xue, C., Song, W., Qin, L., Dong, Q., & Wen, X. (2015). A spatiotemporal mining framework for abnormal association patterns in marine environments with a time series of remote sensing images. International Journal of Applied Earth Observation and Geoinformation, 38, 105–114.

Objectifs

Conception d’un cadre d’exploration de données spatio-temporelles pour des structures d’association marines utilisant de multiples images acquises par télédétection. Le but étant de détecter des événements anormaux basés sur des modèles au niveau des pixels et des objets.

Difficultés

Considérant la taille massive de l’espace de caractéristiques, car chaque pixel possède sa propre structure d’association spatio-temporelle, il est essentiel de trouver un moyen efficace pour découvrir des associations spatio-temporelles marines sur une base pixel par pixel. Le deuxième problème est qu’il faut aussi grouper ces pixels de manière à former des objets analysables.

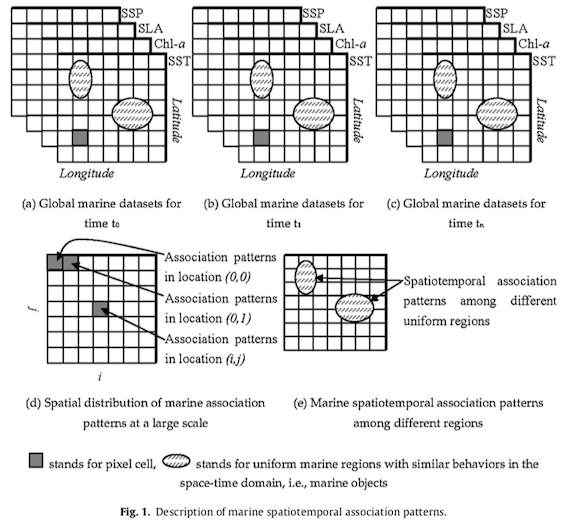
Deux catalogues d’association patterns sont donc générés : dans la même région (pixel, cellule singulière) et entre différentes régions (objet, regroupement de pixels).

La relation spatiale des structures d’association du premier catalogue est simplement le positionnement spatial des pixels. Malgré la faible contribution de ces structures au niveau des relations spatiales, l’utilisation de pixels seulement est plus adaptée pour représenter des structures d’association spatio-temporelles à grande échelle. Dans le contexte de cette étude, ce catalogue permet d’analyser l’océan dans son ensemble.

Pour le deuxième catalogue, les structures d’association entre régions possédant des propriétés marines uniformes (objets marins) fournissent davantage d’information au niveau des relations spatiales : positionnement spatial, distance, direction et topologie. Comparativement au premier catalogue, celui-ci va se concentrer sur des régions marines spécifiques. Les deux catalogues sont donc complémentaires dans la recherche de spatiotemporal association patterns.

Sommaire

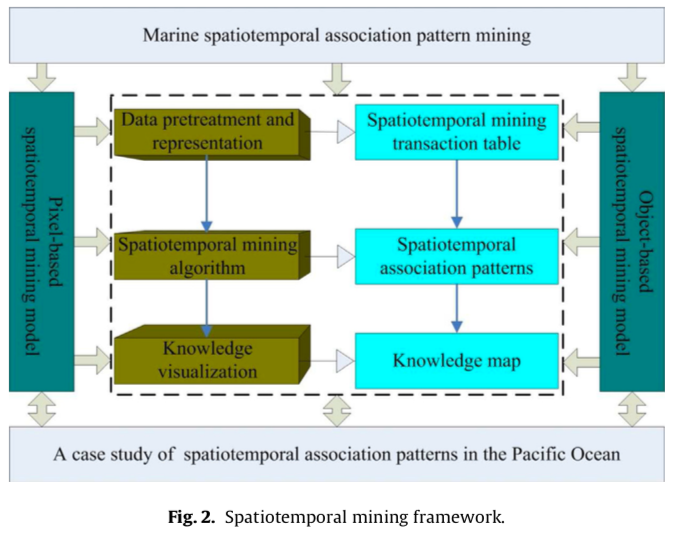
Prétraitement et représentation des données par une table de transaction.
Algorithme d’exploration des données spatio-temporelles pour générer les structures d’association.
Visualisation des connaissances.

Méthode

Prétraitement des données et représentation

Suppression de la variabilité périodique

Les paramètres marins subissent des variations saisonnières : il est donc primordial de supprimer cette composante afin de normaliser les données avant l’identification des événements anormaux. Pour ce faire, le z-score, calculé sur une période mensuelle, est utilisé. Il indique à combien d’écarts-types se situe un paramètre environnemental par rapport à la moyenne et standardise la valeur de ce paramètre en conséquence.

Extraction des objets anormaux

Les régions sensibles aux changements climatiques sont identifiées comme régions anormales et représentées comme objets dans le contexte de cette étude. Le signal ENSO (El Niño-Southern Oscillation) est utilisé pour représenter la variabilité du climat global et les paramètres influencés par ce signal sont identifiés. Pour ce faire, il faut analyser si la composante de temps d’un certain facteur physique est la même que celui d’ENSO (4–7 ans), mais également sa structure spatiale. Par la suite, ces régions sensibles aux changements climatiques et possédant la même structure spatiale associée sont groupées en objets anormaux.

Discrétisation des paramètres marins

La discrétisation consiste à transformer les paramètres marins sous la forme de nombres réels en catégories. La variabilité de l’environnement marin est généralement distribuée de manière gaussienne. Conséquemment, les paramètres sont discrétisés en 5 classes, de -2 à +2 (changement négatif sévère, changement négatif faible, aucun changement, changement positif faible, changement positif sévère).

Où P(i,j) et O sont respectivement la position de pixels et les instances d’objets anormaux, Vi,j et fRank(Vi,j) sont la valeur brute et la classe d’un pixel, Vo et fRank(Vo) sont la valeur brute et la classe d’un objet anormal, 𝛿 et 𝛿o sont l’écart-type d’une série temporelle d’un pixel et d’un objet anormal.

Génération des tables de transactions

Une table d’exploration est générée pour l’analyse à chaque niveau de granularité : pixels et objets. Le premier modèle peut explorer les structures d’association spatio-temporelles parmi les paramètres environnementaux marins au sein des pixels.

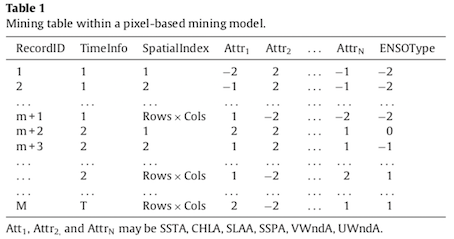
Le deuxième modèle permet de découvrir les structures d’association spatio-temporelles entre les différentes régions marines.

Algorithme d’exploration des données spatio-temporelles

Cet algorithme est basé sur l’information mutuelle, c’est-à-dire la quantité d’information qu’un item fournit à propos d’un autre. Les items sont représentés par les paramètres environnementaux et l’index ENSO (Table 1 et 2). L’index ENSO permet de catégoriser les paramètres marins selon le degré d’influence qu’a le phénomène La Niña (-2) et El Niño (+2) sur leur évolution.

Les algorithmes d’association pattern mining trouvent des règles définissant les relations entre items, en deux étapes. D’abord, ils découvrent l’ensemble de structures d’items fréquents à partir des tables de transactions en utilisant un support minimum. Ensuite, ils généralisent la règle d’association à partir d’un niveau de confiance prédéfini. Seuls les items reliés, plutôt que l’ensemble complet, sont impliqués dans la recherche d’items fréquents.

Extraction d’items reliés

Les items sont considérés comme reliés, ou non, en se basant sur leur information mutuelle normalisée. L’approche mathématique sera mise de côté pour faciliter la lecture. Les items reliés sont extraits pour fournir des candidats à l’ensemble d’items fréquents, qui eux seront utilisés pour trouver les structures d’association. Les items reliés ne sont pas tous retenus pour être des items fréquents : pour ce faire, ils doivent atteindre un certain seuil de relation. L’ensemble d’items fréquents contient toutes les structures d’items qui apparaissent assez fréquemment, selon un seuil, dans l’ensemble de données.

Génération des arbres de structures d’association

Un arbre de structures d’association direct permet de représenter les structures d’association de deux paramètres environnementaux marins ou plus, et ainsi de fournir une fondation pour mettre en place un algorithme d’exploration spatio-temporelle. Une méthode récursive est appliquée pour construire cet arbre.

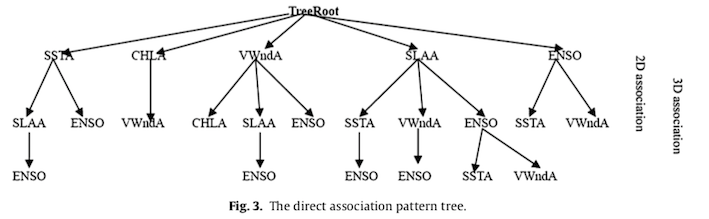
Découverte des règles d’association

La génération des règles d’association permet de découvrir des items fréquents originaires d’arbres de structures d’association directs. Pour y arriver, les tables de transactions et arbres de structures d’association directs sont parcourus à l’aide d’un algorithme d’exploration récursif. Pour généraliser les règles d’association fortes, certains indices d’évaluation sont utilisés : support, confiance, lift et facteurs d’intérêt.

Visualisation des structures d’association spatio-temporelles

Les structures d’association spatio-temporelles sont représentées sous la forme suivante :

Où AttrN est un paramètre environnemental marin d’un pixel ou d’un objet, q est le niveau quantitatif (-2 à +2) de ce paramètre, t est le temps d’occurrence de l’attribut Attr1, {t1, t2 et tn} sont les différences de temps par rapport à t lorsque les autres attributs surviennent, s%, c% et l% sont les indicateurs d’évaluation utilisés pour identifier les structures d’association révélatrices.

Même si les les structures d’association entre les objets et les pixels sont représentées de manière similaire, leurs relations spatiales sont différentes. Les relations spatiales entre objets marins sont implicites ; la topologie, la distance et la direction sont toutes obtenues à partir des objets eux-mêmes. Les relations spatiales entre pixels ne sont pas aussi implicites ; en effet, chaque pixel peut avoir plusieurs structures d’association spatio-temporelles entre deux attributs ou plus.

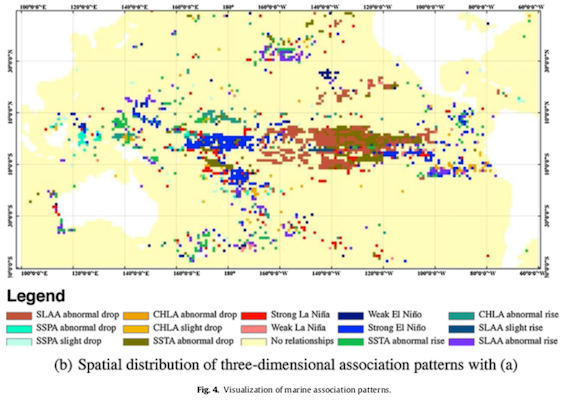
Les structures d’association spatio-temporelles sont visualisées sur les cartes thématiques suivantes. On remarque que les régions blanches définissent les différents continents et les régions colorées les différentes structures d’association dans l’océan pacifique. La carte (a) montre la distribution des structures en deux dimensions, et (b) celle des structures en trois dimensions, comme démontré par l’arbre de structures d’association.

Pour la figure (a), par exemple, on peut voir que lorsque le phénomène La Niña est fort, la température de surface de l’océan (SSTA) chute drastiquement dans la région bleue.

Résultats

L’algorithme de data mining basé sur l’information mutuelle est supérieur à l’algorithme traditionnel Apriori dans le cas où davantage de paramètres et classes sont utilisés lors de la discrétisation.
Deux stratégies sont proposées : un modèle au niveau des pixels et l’autre au niveau des objets. Les deux se complètent : le premier explore les caractéristiques marines à grande échelle et le deuxième se concentre sur des régions précises.
De nombreux problèmes ont été résolus : l’extraction d’items associés (attributs ou objets), la construction d’arbres de structures d’association directs, la conception de l’algorithme d’exploration, le seuil de support optimal et la visualisation innovatrice des structures d’association.
En comparaison aux analyses spatio-temporelles traditionnelles, l’information obtenue à partir de ce cadre d’exploration est beaucoup plus détaillée et précise au niveau de l’espace et du temps.
Ce cadre permet d’améliorer la compréhension de la variation des paramètres marins dans différentes zones : comment, quand et où certains paramètres entraînent la variation d’autres paramètres ou répondent à la variation des autres.