D’une manière générale, un jeu de données (on exclut les données textuelles et les images) comporte deux types de variables : les variables quantitatives et les variables qualitatives.

Une variable quantitative est une variable qui admet des valeurs numériques, continues ou discrètes. Par exemple, la taille d’un individu, le salaire d’un employé, la vitesse d’une voiture sont des variables quantitatives. Ces variables étant numériques, leur traitement par les algorithmes d’apprentissage automatique est plus simple, c’est-à-dire qu’elles peuvent être utilisées directement sans nécessiter une transformation préalable.
Une variable qualitative quant à elle prend des valeurs appelées catégories, modalités ou niveaux qui n’ont pas de sens quantitatif. Par exemple, le genre d’un individu est une variable catégorique avec deux (ou plus) modalités : masculin et féminin. Aussi, des statistiques telles que la moyenne n’ont pas de sens sur ces données. La présence de ces variables dans les données complique généralement l’apprentissage. En effet, la plupart des algorithmes d’apprentissage automatique prennent des valeurs numériques en entrée. Ainsi, il faut trouver une façon de transformer nos modalités en données numériques.
De plus, la façon dont cette transformation est opérée est très importante. En effet, le codage des variables catégoriques nuit généralement à la performance des algorithmes d’apprentissage. Un codage peut s’avérer plus judicieux qu’un autre. Par exemple, les forêts aléatoires, un type d’algorithme d’apprentissage automatique, peinent à capturer l’information des variables catégoriques comportant un grand nombre de modalités si celles-ci sont traitées avec la technique d’encodage one-hot encoding présentée à la section suivante. C’est ainsi que des algorithmes d’apprentissage plus spécifiques tels que Catboost, que nous décrivons plus bas, ont vu le jour.
Dans cet article, nous présentons différentes méthodes et astuces pour gérer les variables catégoriques.
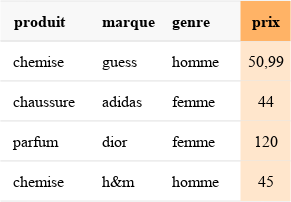
L’exemple ci-dessous sert d’illustration à certaines méthodes tout le long de l’article.
One-hot encoding
Le one hot encoding est la méthode la plus populaire pour transformer une variable catégorique en variable numérique. Sa popularité réside principalement dans la facilité d’application. De plus, pour beaucoup de problèmes, elle donne de bons résultats. Son principe est le suivant :
Considérons une variable catégorique X qui admet K modalités m1, m2, …, mK. Le one hot encoding consiste à créer K variables indicatrices, soit un vecteur de taille K qui a des 0 partout et un 1 à la position i correspondant à la modalité mi. On remplace donc la variable catégorique par K variables numériques.
Si l’on considère l’exemple précédent et qu’on suppose que les catégories disponibles sont uniquement celles affichées, on a alors :
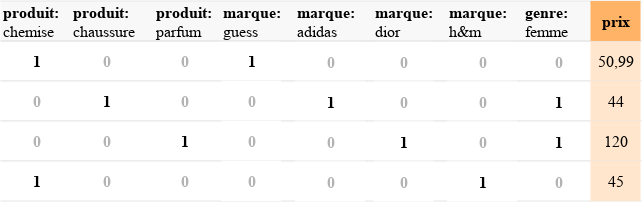
Avantages : simple, intuitif, rapide à mettre en place.
Inconvénients : Lorsque le nombre de modalités est élevé (supérieur à 100 par exemple), le nombre de nouvelles variables créées est également élevé. Ainsi, on se retrouve avec un jeu de données beaucoup plus volumineux, qui occupe plus d’espace en mémoire et dont le traitement par les algorithmes d’apprentissage devient plus difficile. Aussi, certains algorithmes, notamment quelques implémentations des forêts d’arbres décisionnels, n’arrivent pas à exploiter au mieux les informations contenues dans ces variables lorsque ce nombre de modalités est trop grand (voir [1] pour plus de détails).
Réduction du nombre de modalités
La connaissance métier peut aider à réduire le nombre de modalités. En effet, une compréhension des catégories peut permettre de les regrouper efficacement. Un regroupement naturel se fait lorsque les modalités sont hiérarchiques, c’est-à-dire qu’il est possible de définir une nouvelle catégorie qui englobe d’autres catégories. Supposons une variable dont les catégories sont les quartiers d’une ville : ces catégories peuvent par exemple être regroupées par arrondissement, c’est-à-dire que les quartiers d’un même arrondissement auront la même modalité. Il s’agit d’un cas assez fréquent. Toutefois, signalons que ces regroupements peuvent introduire un biais dans le modèle.
Une seconde façon de s’en tirer avec un nombre de catégories élevé consiste à essayer de fusionner les modalités à faible effectif. On peut combiner les modalités qui apparaissent très peu fréquemment dans les données. On effectue un tableau des effectifs des modalités, et celles dont la fréquence est inférieure à un certain seuil sont mises ensemble dans une même catégorie «autre» par exemple. Ensuite, un one-hot encoding peut être appliqué sur la nouvelle variable.
Variables ordinales
Les variables ordinales sont des variables catégoriques qui présentent une notion d’ordre, c’est-à-dire qu’un classement de leurs modalités est possible. Par exemple, la variable Tranche d’âge qui prendrait les valeurs bébé, adolescent, enfant, adulte, personne âgée est une variable ordinale. En effet nous pouvons ordonner les modalités de manière croissante comme suit : bébé < enfant < adolescent < adulte < personne âgée.
Dans le cas de telles variables, une alternative au one-hot-encoding consiste à utiliser le rang pour encoder les modalités, ce qui rend alors la variable quantitative. Dans l’exemple Tranche d’âge, nous aurions par exemple bébé = 1, enfant = 2, adolescent=3, etc.
La connaissance des modalités peut permettre d’associer d’autres valeurs numériques aux modalités, autre que le rang. Dans le cas de Tranche d’âge, nous savons que l’adolescence va d’environ 12 à 17 ans, l’âge adulte de 25 à 65 ans. Ainsi la moyenne ((12 +17) / 2 = 14.5) de la plage de valeurs peut être préférée au rang.
Les jours de la semaine et les jours du mois peuvent être également traités comme des variables ordinales.
Impact encoding
Lorsque le nombre de catégories devient très grand l’encodage par variables indicatrices peut devenir incommode. Une méthode alternative au clustering ou à la troncation des catégories consiste à caractériser les catégories par le lien qu’elles entretiennent avec la variable cible y : il s’agit de l’impact encoding.
Cette méthode est aussi connue sous les noms : likelihood encoding, target coding, conditional-probability encoding, weight of evidence ([9]).
Définition : Pour un problème de régression ayant pour variable cible y, soit X, une variable catégorique ayant K catégories m1, …, mK. Chaque catégorie mk est encodée par sa valeur d’impact :
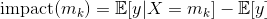
𝔼[y|X=mk] correspond à l’espérance de la cible y sachant que la variable X est fixée à la modalité mk. Pour un jeu d’entraînement de taille n contenant des échantillons {(xi, yi), 1≤i≤n} indépendants et identiquement distribués, l’estimateur de cette espérance est la moyenne des valeurs de yi pour lesquelles la modalité xi est égale à mk :
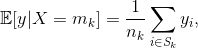
où Sk est l’ensemble des indices i des observations telles que xi soit égal à mk et nk la cardinalité de cet ensemble.
L’estimateur de l’espérance de y est simplement sa moyenne empirique :
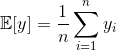
Notons qu’il existe d’autres variantes à la définition donnée ci-haut. Par exemple, dans [8], les deux expressions sont pondérées par un paramètre compris entre 0 et 1.
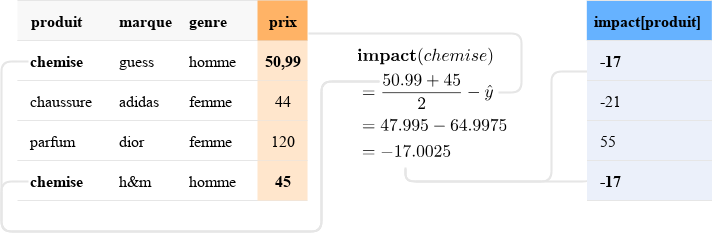
Pour illustrer l’impact encoding, considérons la variable produit dans notre exemple précédent. Elle a trois modalités, à savoir chemises, chaussures et parfums. La moyenne empirique est (50,99 + 44 + 120 + 45)/4 = 64,9975. On a alors :
impact(chemises) = (50,99 + 45)/2–64,9975 = -17
impact(chaussures) = 44–64,9975 = -21
impact(parfum) = 120–64,9975 = 55
Cet encodage a l’avantage d’être très compact : le nombre de descripteurs d’une variable est constant par rapport au nombre de catégories. Cependant, cet encodage entraîne une perte d’information : seule une valeur de «corrélation» avec la cible y est retenue. Cela signifie que si deux catégories ont des valeurs proches pour la cible y en moyenne, elles ne pourront pas être distinguées par le modèle.
Pour remédier à cette perte d’information, il est possible de garder des variables indicatrices pour les catégories les plus dominantes. Une alternative est d’encoder des combinaisons de variables : parfois, une catégorie seule ne sera pas corrélée avec la cible y, mais la combinaison de deux variables catégoriques peut être «prédictive» de la cible. En pratique, cela consiste à identifier les paires (voire triplets) de variables catégoriques qui peuvent avoir une interaction avec la variable cible et encoder la concaténation des instances de ces variables; une connaissance métier aide souvent à identifier ces combinaisons de variables intéressantes. Cette méthode peut même être étendue à l’encodage des variables non catégoriques, en transformant les variables continues en variables binaires, par discrétisation et binarisation ([6], [7]).
L’impact encoding est une forme de model stacking (empilement de modèles) : dans un premier temps, des modèles simples (calculs des 𝔼[y|xk]) sont entraînés sur chacune des variables catégoriques. Les prédictions en sortie de ces modèles sont alors utilisées comme descripteurs dans un second modèle.
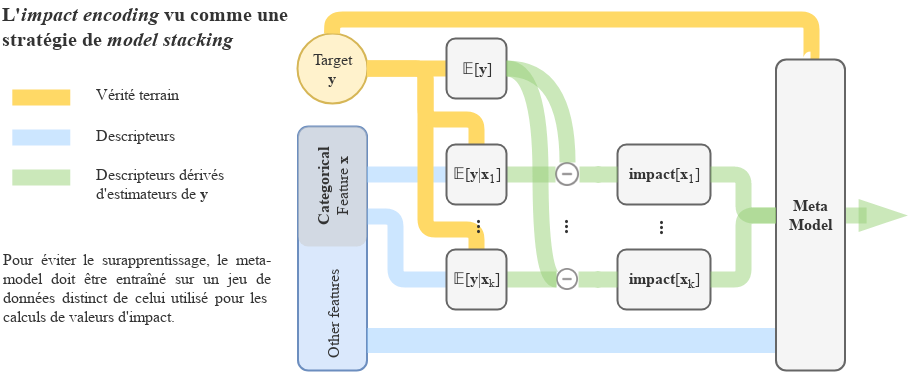
Comme pour toute méthode de stacking, il y a un fort risque de surapprentissage. En effet, les nouveaux descripteurs peuvent être très corrélés à la cible, donnant ainsi des résultats trop optimistes. Il convient alors de calculer l’impact sur un petit jeu de données distinct du jeu d’entraînement utilisé pour le modèle. Habituellement une méthode de cross-validation (validation croisée) est utilisée.
Une application de ces méthodes est faite dans Catboost, une implémentation de l’algorithme de gradient boosting maintenu par Yandex. Par défaut, toutes les variables catégoriques avec plus de deux catégories sont encodées par impact encoding (ou variantes).
Dans Catboost, l’impact encoding n’est réalisé qu’avec des variables cibles binaires (0/1). Dans le cas où le problème n’est pas une classification binaire, la variable cible est transformée en plusieurs variables binaires et, pour chacune de ces variables, un encodage par impact est réalisé. Par exemple, si pour un problème de classification, la variable cible est catégorique, elle est convertie en K variables binaires par encodage one-hot.
Avantages : Le nombre de descripteurs produit ne dépend pas du nombre de catégories. C’est une forme d’encodage relativement simple.
Inconvénients : Une complexité d’implémentation due au risque de surapprentissage (l’utilisation de bibliothèques comme vtreat ou catboost est recommandée).
Méthodes d’embeddings
Cette méthode utilise des techniques de l’apprentissage profond; elle tire son inspiration de modèles comme word2vec sur les données textuelles et qui donnent des résultats très impressionnants.
Il s’agit de créer une représentation de chaque modalité d’une variable catégorique en un vecteur numérique de taille fixe (e par exemple). Ainsi la modalité dior de la variable marque de notre exemple peut être représentée par le vecteur (0,54, 0,28) pour e=2 par exemple. L’utilisation des embeddings permet entre autres une réduction de la dimensionnalité puisque la taille du vecteur e peut être choisie très petite par rapport au nombre de modalités. En effet, plutôt que de créer une variable pour chaque modalité, ici seulement e variables sont créées.
Concrètement, l’obtention de ces embeddings se fait par l’entraînement d’un réseau de neurones (souvent un perceptron multicouche) avec en entrée uniquement les variables catégoriques. D’abord, un one-hot encoding est appliqué à la variable afin d’être mise en entrée du réseau. Généralement, une ou deux couches cachées sont suffisantes. La première couche cachée possède e neurones. Le réseau est alors entraîné sur la même tâche que celle initialement définie. Puis, la sortie de la première couche cachée constitue alors le vecteur d’embeddings ([10]). On concatène ensuite ce vecteur aux données initiales (création de e variables). Ces données sont ensuite utilisées dans l’ajustement du modèle final. Il existe dans la littérature diverses variantes sur la manière d’obtenir ces embeddings. En outre, rien n’empêche de mettre plus de deux couches cachées et de retenir la sortie de la deuxième plutôt que celle de la première. Par ailleurs, le réseau peut être entraîné sur une tâche autre que la tâche initiale.
Avantages : Les embeddings permettent une réduction de la dimension; dans certains cas, leur utilisation donne des performances nettement meilleures. De plus, ils peuvent permettre d’éviter l’introduction de biais lors de la réduction des modalités par la connaissance métier.
Inconvénients : La nécessité d’entraîner un réseau de neurones peut freiner certains utilisateurs (peu familiers avec l’apprentissage profond), surtout si le modèle final retenu est un modèle simple comme une régression linéaire. Aussi, on perd en interprétabilité des variables catégoriques.
Conclusion
Les variables catégoriques sont très fréquentes dans les données et il faut leur accorder une attention minutieuse. En effet, leur traitement adéquat peut permettre d’améliorer considérablement les performances d’un modèle. Il est important de noter que les techniques présentées ici ne sont que quelques stratégies à explorer et qu’il en existe beaucoup d’autres. Aussi, face à une nouvelle tâche, il faut tester les différents encodages pour voir celles qui donnent les meilleurs résultats.
Références
- https://roamanalytics.com/2016/10/28/are-categorical-variables-getting-lost-in-your-random-forests/
- vtreat: a data.frame Processor for Predictive Modeling , article associé à la bibliothèque de génie de descripteurs vtreat, utilisé comme principale référence de ce billet : https://arxiv.org/pdf/1611.09477.pdf
- Transforming categorical features to numerical features, de la documentation de Catboost : https://tech.yandex.com/catboost/doc/dg/concepts/algorithm-main-stages_cat-to-numberic-docpage/
- Tutoriel sur l’impact encoding de variables catégorielles : https://github.com/Dpananos/Categorical-Features
- Efficient Estimation of Word Representations in Vector Space : https://arxiv.org/pdf/1301.3781.pdf
- Page «binarization» de la documentation de Catboost : https://tech.yandex.com/catboost/doc/dg/concepts/binarization-docpage/
- https://books.google.fr/books?id=MBPaDAAAQBAJ&pg=PT102#v=onepage&q&f=false
- https://kaggle2.blob.core.windows.net/forum-message-attachments/225952/7441/high%20cardinality%20categoricals.pdf
- Weight of Evidence, un outil surtout utilisé en économétrie, analogue à l’impact encoding : https://www.listendata.com/2015/03/weight-of-evidence-woe-and-information.html
- Entity Embeddings of Categorical Variables : https://arxiv.org/pdf/1604.06737.pdf
- https://commons.wikimedia.org/wiki/File:Perceptron_4layers.png








