Broadly speaking, a dataset (excluding textual data and images) has two types of variables: quantitative and qualitative.

A quantitative variable is a variable that admits numerical values, continuous or discrete. For example, the height of an individual, the salary of an employee, and the speed of a car are quantitative variables. As these variables are numerical, their treatment by machine learning algorithms is more straightforward, i.e. they can be used directly without requiring a prior transformation.
A qualitative variable takes on values called categories, modalities or levels that have no quantitative meaning. For example, the gender of an individual is a categorical variable with two (or more) modalities: male and female. Also, statistics such as the mean do not make sense in this data. The presence of these variables in the data generally complicates learning. Indeed, most machine learning algorithms take numerical values as input. Thus, we must find a way to transform our modalities into numerical data.
Moreover, how this transformation is carried out is very important. Indeed, the coding of categorical variables generally affects the performance of learning algorithms, and one type of coding may be more appropriate than another. For example, random forests, a type of machine learning algorithm, have difficulty capturing the information of categorical variables with a large number of modalities if treated with the one-hot encoding technique presented in the next section. Thus, more specific learning algorithms, such as Catboost, which we describe below, have emerged.
This article presents different methods and tips for managing categorical variables.
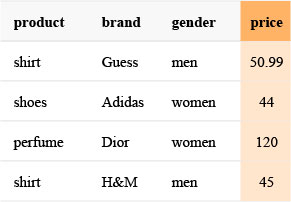
The example below serves as an illustration of some methods throughout the article.
One-hot encoding
One-hot encoding is the most popular method for transforming a categorical variable into a numerical variable. Its popularity lies mainly in the ease of application. Moreover, for many tasks, it gives good results. Its principle is as follows:
Let us consider a categorical variable X which admits K modalities m1, m2, …, mK. One-hot encoding consists in creating K indicator variables, i.e. a vector of size K which has 0’s everywhere and a 1 at position i corresponding to the modality mi. We thus replace the categorical variable with K numerical variables.
If we consider the previous example and assume that the available categories are only those displayed, we then have:
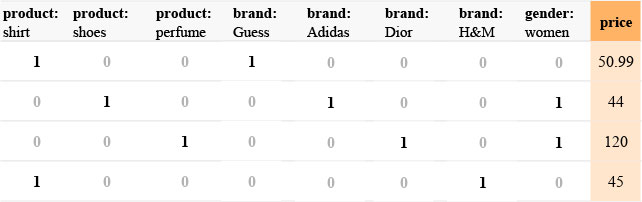
Advantages: simple, intuitive, and quick set up.
Disadvantages: When the number of modalities is high (more than 100 for example), the number of new variables created is also high. Thus, we end up with a much larger dataset, which occupies more memory space and whose processing by the learning algorithms becomes more difficult. Also, some algorithms, in particular some implementations of decision tree forests, do not best use the information contained in these variables when the number of modalities is too great (see [1] for more details).
Reduction in the number of modalities
In-depth knowledge can reduce the number of modalities. Indeed, an understanding of the categories can enable them to be grouped efficiently. A natural grouping occurs when the categories are hierarchical, i.e. it is possible to define a new category that includes other categories. Suppose a variable whose categories are a city’s neighbourhoods: these categories can, for example, be grouped by borough, i.e., the neighbourhoods of the same borough will have the same modality. This is a relatively common situation. However, we should point out that such groupings may introduce a bias in the model.
A second way to get by with a high number of categories is to try to merge modalities with low numbers. Modalities that appear very infrequently in the data can be combined. A table of the number of modalities is made, and those whose frequency is lower than a certain threshold are put together in the same category, “other” for example. An on-hot encoding can then be applied to the new variable.
Ordinal variables
Ordinal variables are categorical variables that show a notion of order, i.e. a ranking of their modalities is available. For example, the variable Age Range, which would take the values baby, adolescent, child, adult, and elderly, is an ordinal variable. Indeed we can order the modalities ascendingly as follows: baby < child < teenager < adult < elderly.
In the case of such variables, an alternative to one-hot-encoding is to use the rank to encode the modalities, which then makes the variable quantitative. In the Age Range example, we would have, for instance, baby = 1, child = 2, teenager=3, etc.
Knowing the modalities can allow us to associate numerical values other than rank. In the case of Age Range, we know that adolescence runs from about 12 to 17 years and adulthood from 25 to 65 years. Thus the mean ((12 +17) / 2 = 14.5) of the range of values can be used instead of rank.
Days of the week and days of the month can also be treated as ordinal variables.
Impact encoding
Encoding by indicator variables may become inconvenient when the number of categories becomes very large. An alternative method to clustering or truncating categories consists of characterizing the categories by their link with the target variable y: this is called impact encoding.
This method is also known as likelihood encoding, target coding, conditional-probability encoding, and weight of evidence ([9]).
Definition: For a regression problem with target variable y, say, X, a categorical variable with K categories m1, …, mK. Each category mk is encoded by its impact value:
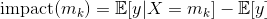
𝔼[y|X=mk] is the expectation of the target y, knowing that the variable X is set to modality mk. For a training set of size n containing independent and identically distributed samples {(xi, yi), 1≤i≤n}, the estimator of this expectation is the average of the values of yi for which the modality xi is equal to mk:
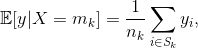
Where Sk is the set of indices i of the observations such that xi is equal to mk and nk is the cardinality of this set.
The estimator of the expectation of y is simply its empirical mean:
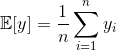
Note that there are other variants to the definition given above. For example, in [8], both expressions are weighted by a parameter between 0 and 1.
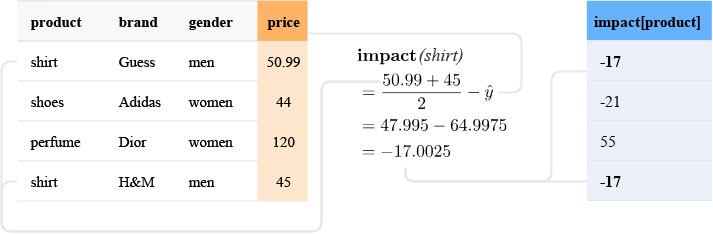
To illustrate impact encoding, let us consider the product variable in our previous example. It has three modalities, namely shirts, shoes and perfumes. The empirical mean is (50.99 + 44 + 120 + 45)/4 = 64.9975. We then have:
Impact (shirts) = (50,99 + 45)/2–64,9975 = -17
Impact (shoes) = 44–64,9975 = -21
Impact (perfume) = 120–64,9975 = 55
This encoding has the advantage of being very compact: the number of descriptors of a variable is constant compared to the number of categories. However, this encoding leads to a loss of information: only a “correlation” value with the target is retained. This means that if two categories have close values for the target y on average, the model cannot distinguish them.
To remedy this loss of information, indicator variables can be kept for the most dominant categories. Alternatively, it is possible to encode combinations of variables. Sometimes, a category alone will not be correlated with the target y, but the combination of two categorical variables can be “predictive” of the target. In practice, this consists in identifying the pairs (or even triplets) of categorical variables that can interact with the target variable and encode the concatenation of the instances of these variables; in-depth knowledge often helps to identify these interesting combinations of variables. This method can even be extended to the encoding of non-categorical variables by transforming continuous variables into binary variables, by discretization and binarization ([6], [7]).
Impact encoding is a form of model stacking: first, simple models (𝔼[y|xk] calculations) are trained on each of the categorical variables. The output predictions of these models are then used as descriptors in a second model.
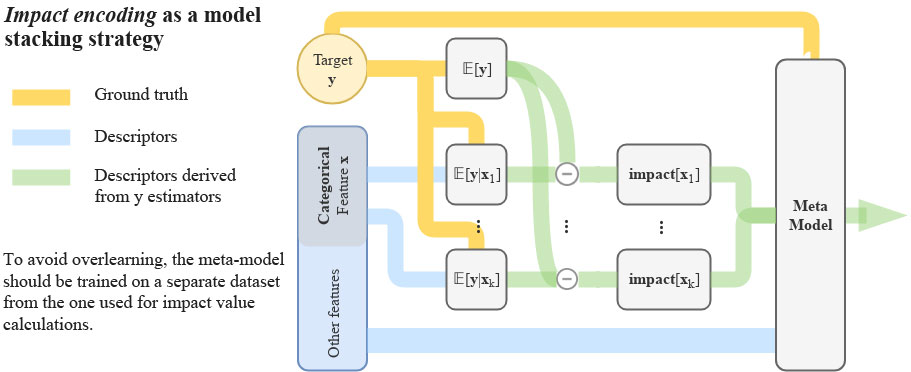
As for any stacking method, there is a substantial risk of overlearning. Indeed, the new descriptors can be highly correlated to the target, giving overly optimistic results. It is then necessary to calculate the impact on a small data set distinct from the training set used for the model. Usually, a cross-validation method is used.
These methods are applied in Catboost, an implementation of the gradient boosting algorithm maintained by Yandex. By default, all categorical variables with more than two categories are encoded by impact encoding (or variants).
In Catboost, impact encoding is only performed with binary target variables (0/1). In a case where the problem is not a binary classification, the target variable is transformed into several binary variables, and, for each of these variables, an impact encoding is performed. For example, if, for a classification problem, the target variable is categorical, it is converted into K binary variables through one-hot encoding.
Advantages: The number of descriptors produced does not depend on the number of categories; this is a relatively simple form of encoding.
Disadvantages: Complex implementation due to the risk of overlearning (libraries like vtreat or catboost are recommended).
Methods of embedding
This method uses deep learning techniques; it draws inspiration from models like word2vec on textual data and yields very impressive results.
It consists of creating a representation of each modality of a categorical variable in a fixed-size numerical vector (e, for example). Thus the Dior modality of the brand variable in our example can be represented by the vector (0.54, 0.28) for e=2, for instance. The use of embeddings allows, among other things, a reduction in dimensionality since the size of the vector e can be selected to be very small compared to the number of modalities. Indeed, rather than creating a variable for each modality, only e variables are created.
Concretely, these embeddings are obtained by training a neural network (often a multilayer perceptron) with only categorical variables as input. First, a one-hot encoding is applied to the variable in order to be put into the network input. Generally, one or two hidden layers are sufficient. The first hidden layer has e neurons. The network is then trained on the same task as the one initially defined. Then, the output of the first hidden layer constitutes the vector of embeddings ([10]). This vector is subsequently concatenated with the initial data (creation of e variables). These data are then used in the final model fitting. There are different variants in the literature on how to obtain these embeddings. Moreover, nothing prevents one from putting more than two hidden layers and retaining the output of the second rather than the first. Also, the network can be trained on a task other than the initial one.
Advantages: Embeddings allow a reduction of the dimension; in some cases, their use gives significantly better performances. In addition, they can avoid introducing bias during the reduction of modalities through in-depth knowledge.
Disadvantages: The need to train a neural network may slow down some users (unfamiliar with deep learning), especially if the final model selected is a simple model such as linear regression. Also, we lose the interpretability of categorical variables.
Conclusion
Categorical variables are widespread in data and should receive careful attention. Indeed, their proper treatment can significantly improve the performance of a model. It should be noted that the techniques presented here are only a few strategies to explore and that there are many others. Also, when faced with a new task, it is necessary to test the different encodings to see which ones give the best results.
References
- https://roamanalytics.com/2016/10/28/are-categorical-variables-getting-lost-in-your-random-forests/
- vtreat: a data.frame Processor for Predictive Modeling, an article associated with the vtreat descriptor engineering library, used as the primary reference for this post: https://arxiv.org/pdf/1611.09477.pdf
- Transforming categorical features to numerical features, from Catboost documentation: https://tech.yandex.com/catboost/doc/dg/concepts/algorithm-main-stages_cat-to-numberic-docpage/
- Tutorial on impact encoding for categorical variables: https://github.com/Dpananos/Categorical-Features
- Efficient Estimation of Word Representations in Vector Space: https://arxiv.org/pdf/1301.3781.pdf
- “Binarization” page of the Catboost documentation: https://tech.yandex.com/catboost/doc/dg/concepts/binarization-docpage/
- https://books.google.fr/books?id=MBPaDAAAQBAJ&pg=PT102#v=onepage&q&f=false
- https://kaggle2.blob.core.windows.net/forum-message-attachments/225952/7441/high%20cardinality%20categoricals.pdf
- Weight of Evidence, a tool mainly used in econometrics, is similar to impact encoding: https://www.listendata.com/2015/03/weight-of-evidence-woe-and-information.html
- Entity Embeddings of Categorical Variables: https://arxiv.org/pdf/1604.06737.pdf
- https://commons.wikimedia.org/wiki/File:Perceptron_4layers.png









